
Denis Jardim Villarinho - Prof. Dr. M.Sc. Eng. Mec. Conselheiro da Câmara Especializada de Engenharia Mecânica e Metalúrgica do CREA-RS.
André Gandolfi - Engenheiro Mecânico - Empresa Contratec Ltda.
Elton Stein - Engenheiro Mecânico - PLH Empresa Contratec Ltda.

Análise Parcial de Vaso de Pressão Cilíndrico de Parede Fina, Fabricado em Aço
1 - INTRODUÇÃO
Os vasos de pressão são reservatórios utilizados nas indústrias petrolíferas, farmacêutica, siderúrgica, alimentícia e outras, para armazenar transportar, processar líquidos e gases sob pressão na faixa de 1,02 Kgf/cm2 a 200 Kgf/cm2 e pressão externa (vácuo), (ASME 2010). As normas frequentemente utilizadas no Brasil para projeto, inspeção, manutenção são: ASME (American Society of Mechanical Engineers), Seção VIII, Divisão 1 (Pressure Vessel Boiler Code), código para caldeira e vasos de pressão. API 579, BS 7910, NR 13. A Portaria MTP no. 1846 de 01.07.2022 aprova a nova redacao da NR-13. O objetivo deste artigo é verificar de maneira suscinta as características do casco de um vaso de pressão, cilíndrico de seção constante.
2 - REVISÃO BIBLIOGRÁFICA
Os vasos de pressão devem ter uma placa de identificação fornecida pelo fabricante onde devem constar informações importantes tais como, fabricante, pressão do teste hidrostático, PMTA (pressão máxima de trabalho admissível), data de sua fabricação, código de projeto e ano de edição (NR-13, 2022). Com os dados da placa são refeitos os cálculos de construção do vaso.
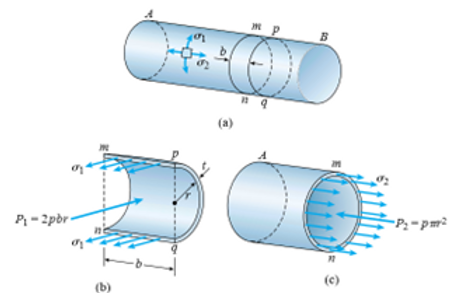
Figura 1: Principais tensões que ocorrem em um vaso de pressão são a tensão circunferencial σ1 a tensão longitudinal σ2 e a tensão radial σ3.
MATÉRIA DE CAPA
.jpg)
PALAVRA DA PRESIDENTE

ARTIGOS

CIVIL
INOVAÇÕES TECNOLÓGICAS

FISCALIZAÇÃO

Fonte – Gere, 2004 Tensões atuantes em um vaso cilíndrico.
2.1 - MATERIAIS, TEMPERATURA DE PROJETO, PRESSÃO DE PROJETO E TENSÃO ADMISSÍVEL
A tensão circunferencial gerada pela pressão de projeto deve ficar abaixo da tensão de escoamento do material.
Para aço carbono ou aço baixa liga utiliza-se a tabela UCS-23 do Código ASME B31.
Ao escolher aço tabelado, a tabela fornece a tensão admissível do material em relação a temperatura de projeto. Quando há diferentes temperaturas, pressões e tensões admissíveis, através de cálculo e escolhida a condição mais severa em relação a tensão admissível, para assim determinar a pressão de projeto, a temperatura de projeto, e a tensão admissível do projeto. Observa-se no cálculo que a norma ASME permite acrescentar de 300C a 50 ºC as temperaturas. Para tensões de projeto assume-se que as falhas em um vaso de pressão sujeitas a pressão interna ocorrem por tensões de tração que acontecem tangencialmente as paredes do vaso.
As tensões de projeto conforme Mott e Untener, 2018, para pressão constante pode ser baseada na tensão de escoamento do material, sendo a equação dada por σd=Sy / N onde σd=tensão de projeto; Sy=tensão de escoamento e N=fator de projeto, que é frequentemente ditado por normas devido ao perigo oferecido quando o vaso de pressão falha, particularmente para gases e vapor sob pressão. Na ausência de normas especificas é possível usar N=4 como valor mínimo e maiores para aplicações onde há incerteza nas condições de operação e propriedades do material. Outra prática sugerida e limitar a pressão interna do vaso em não mais de 1 / 6 da pressão onde ocorrerá a ruptura, colapso (explosão) do vaso, isso relaciona a tensão de projeto a tensão de tração do material, que e mostrado na equação σd= Su / N ou Su / 6 onde Su=tensão de tração. Também, utiliza-se N=8 no mínimo para relacionar a resistência a fadiga do material.
2.2 - FORMATO DO VASO DE PRESSÃO
Os formatos usuais são o cilíndrico e o esférico, esse trabalho é focado em vasos cilíndricos. As equações para o cálculo analítico são diferentes para os dois casos.
2.3 - FABRICAÇÃO DO VASO
Tubos com costura ou sem costura. Importante no desenvolvimento dos cálculos, pois os tubos com costura são calandrados e soldados e os tubos sem costura são extrudados, o que acarreta diferentes resistências.
.png)
2.4 ESPESSURA DO VASO DE PRESSÃO
O material, a tensão admissível e a espessura são os parâmetros mais importantes para o desenvolvimento dos cálculos ao adequar as normas. A espessura pode ser medida com ultrassom no caso de vasos em operação. Nos vasos em operação podem ocorrer uma estenose, ou estreitamento do diâmetro interno com a perda de espessura devido a corrosão, o que altera toda a planilha de projeto. A começar pela PMTA, a pressão máxima de trabalho admissível e por consequência a regulagem da PSV, pressure safety valve do teste hidrostático.
Com a tensão admissível calcula-se a espessura e com o diâmetro médio verifica-se se o vaso se enquadra em vasos de parede grossa ou parede fina, pois há diferentes equações para os dois casos. Se Dm / t >=20 (Dm é o diâmetro médio), vaso é de espessura fina, caso não atenda a relação a espessura é grossa.
Equações para espessura mínima segundo a ASME B 31 (Telles, P.S., 1999).
t= (PxDo) / 2(ShE+PY) +C ou t= (Pxdi) /2(ShE+PY-P) +C
Onde t=espessura ; P=pressão interna de projeto ; Sh=tensão admissível na temperatura de projeto; Do=diâmetro externo e di=diâmetro interno. (ASME B31) (Telles, P.S, 1999).
No cálculo da espessura considerações como E, coeficiente de solda para tubos com costura que varia de 0,8 a 1,0 e para tubos sem costura E=1,0.
Y= coeficiente de redução de acordo com o material e a temperatura do tubo.
C= soma das margens para corrosão, erosão, e aberturas de roscas e de chanfros.
C= 0,05” para aço carbono. (Telles, P.S, 1999).
O E não deve ser confundido com o modulo de Young dos materiais.
2.5 PMTA
A tensão circunferencial gerada pela pressão da PMTA deve ficar abaixo da tensão de escoamento do material e igual a tensão admissível.
A PMTA do vaso para cascos cilíndricos de pequena espessura.
P=(S x E x t)/R + (0,6 x t) onde t=espessura; S=tensão admissível para a condição calculada.; R= raio interno; E= coeficiente de solda. A PMTA de cada parte de um vaso e a pressão que causa na parte em questão uma tensão máxima igual a tensão admissível do material na temperatura de operação correspondente à parte considerada (Telles, P.S. 1991).
2.6 PSV (Pressure Safety Valve).
A tensão circunferencial gerada pela pressão da PSV deve ficar abaixo da tensão de escoamento do material.
A pressão regulada na PSV é igual ou inferior a pressão da PMTA calculada conforme (NR-13. 2014, 2017).
2.7 TESTE HIDROSTÁTICO.
PTH=1,3xPMTA (NR-13).
A tensão circunferencial gerada pela pressão do teste hidrostático deve ficar abaixo da tensão de escoamento do material e logo acima da tensão admissível.
Teste hidrostático é um ensaio realizado em vasos de pressão para detectar se há vazamentos, rupturas, ou deformações significativas. Estes ensaios são realizados com equipamento fora de operação pressurizados com fluido incompressível, até uma grandeza 1,3 vezes a pressão máxima de trabalho admissível (PMTA) simulando uma situação mais rigorosa que a de operação normal para assim garantir que não haverá colapso do equipamento, após 30 minutos de pressurização a pressão e reduzida em 1/3 e verifica-se visualmente se houve vazamento ou ruptura. O teste hidrostático é considerado não destrutivo exigido pela ASME e deve ser realizado sempre que um equipamento for fabricado, ou no campo antes do início de operação e observadas as disposições complementares da NR-13. Até o ano de 2004 esse teste usava o valor de 1,5xPMTA, após a mudança na norma esse valor passou a ser 1,3xPMTA.
2.8 TENSÕES CIRCUNFERENCIAL, LONGITUDINAL E RADIAL (GROEHS, 2006).
As tensões também podem ser calculadas pelas seguintes equações:
σcirc= p x ((re2+ ri2) / (re2-ri2)) σlong= (p x ri2 ) / (re2-ri2)) σrad= -p
re= raio externo ri= raio interno p=pressão

3 METODOLOGIA SEGUIDA DE RESULTADOS DEMONSTRATIVOS EM ESTUDO DE CASO
Abaixo segue um exemplo ilustrativo da verificação de um tanque em aço, contendo oxigênio com pressão interna (p) de 2,0 MPa. O tanque mede diâmetro externo do= 450,0mm e espessura de parede (t) com 10,0mm. Verificar o tanque calculando a tensão a circunferencial, σ1, tensão longitudinal, σ2, indicando a tensão radial, σ3, com a tensão circunferencial calcular a tensão de escoamento mínimo que deve ter o material, assim encontrar em tabela o provável aço e indicar sua máxima tensão, de tração, escolhendo o aço na medida calculada ou o mais próximo de tabela. Com a tensão máxima de tração extraído de tabela, calcular a provável pressão de explosão, com esses dados é concluído com a indicação da provável pressão de trabalho no tanque. (ASME B31, 2010) (Mott e Untener, 2018).
Solução:
a) Cálculo do diâmetro médio do tanque (Dm): Dm = Do - t = 450,0 – 10 = 440,0mm.
b) Verificação de parede fina ou parede grossa segundo ASME B31, Dm / t > 20, logo indicando ser parede fina.
c) Como é parede fina a tensão circunferencial pode ser calculada pela equação σ1 = (p x Dm) / 2t logo σ1=(2 x440) / (2x10) = 44,0Mpa.
d) A tensão longitudinal é calculada pela equação σ2 = (p x Dm)/4t então σ2 = (2 x 440) / (4 x 10) = 22,0Mpa.
e) A tensão radial é a pressão interna σ3=-p ou σ3= -2Mpa.
f) A norma ASME B31 permite calcular a tensão de escoamento mínimo do material (Sy) através da equação Sy= Nxσ1 onde N é fator de projeto, conforme revisão bibliográfica acima, logo Sy=4x44,0=176 Mpa, essa seria a tensão de escoamento mínima, o que recairia em alguns materiais não-ferrosos e como o enunciado indica ser aço, consultando a tabela de aços (Gerdau) com suas propriedades mecânicas, e encontrado o valor de Sy tensão de escoamento de 285MPa, um valor bem acima do calculado que e 176 MPa. Seria o aço SAE 1015 recozido com tensão de tração Su=385 MPa e dureza Brinell 111HB. Nesse caso seria importante, informação do fabricante para confirmar o material, ou se fosse tanque descartado um teste de dureza e metalografia de amostra para confirmar se é um aço de menor teor de carbono. Note-se que a tabela Gerdau consultada começa com SAE 1015.
g) Assumindo que o aço é SAE 1015, com tensão de tração Su=385 MPa, calcula-se a pressão de explosão pex, igualando-se a tensão circunferencial calculada σ1 a tensão máxima de tração. Logo pex= (Su x 2t)/ Dm onde p= (385x20)/440= 17,5MPa.
h) O fator de projeto 6 e usualmente aplicado na pressão de explosão afim de se obter a pressão de operação permitida, logo o cilindro deverá ser limitado no máximo 17,5 / 6 = 2,9 MPa.
i) Assumindo aço SAE 1015 tensão de escoamento 285 e fator N=4 a PMTA e
E=1,0 e (Do-2t) = di ; 450-20=430 logo Ri = 215 ; S = 285/4 = 71,25
PMTA = (71,25 x 1x 10) / (215+0,6.10) = 712,5/221 = 3,2MPa ; PSV=3,2 MPa
j) PTH = 1,3 x PMTA = 4,16MPa
4 CONCLUSÃO
Este trabalho conforme o título é uma verificação parcial dos principais parâmetros que guiam a análise de um vaso de pressão.
Uma verificação completa e profunda deve ser feita em casos como análise de falhas, do vaso, exigindo as vezes, ensaios de dureza HB, HRB, Vickers, metalografia, Rx, difração de Rx, ultrassonografia. Análise minuciosa em todos os pontos de solda com os devidos cálculos de PMTA em cada ponto, inclusive nos tampos (heads). O que já seria um roteiro de inspeção do vaso ou uma perícia. Atualmente muitos softwares têm sido usados, associados a cálculos de elementos finitos. O caráter pedagógico desse trabalho da ênfase no cálculo analítico, que o engenheiro deve proceder e comparar com os softwares utilizando esses como ferramenta auxiliar.
Como visto, nos cálculos o tanque em foco trabalha com 2,0 MPa, sendo a pressão recomendada não passar de 2,9 MPa.
Após um teste hidrostático, o mais agressivo, uma análise visual verificando que não houve vazamentos ou deformações plásticas aparentes já e um indício de bom estado do tanque. Se fosse previsto alguma falha essa provavelmente seria por fadiga ou falha de componentes.
A provável pressão de explosão foi calculada em 17,5 MPa utilizando-se fator de projeto N=4 e tensão de tração do material, o que dá segurança na escolha do material.
Observa-se que nos cálculos de projetos de vasos de pressão, as pressões PMTA, PSV, teste hidrostático provocam tensões circunferenciais abaixo da tensão de escoamento, ou seja, dentro da zona elástica do material, o que dá segurança ao projeto.
Provável quadro final da análise:
Material escolhido para a aplicação = SAE 1015.
Sy= 285 MPa
Su= 385 MPa
Do=450,0 mm
Di= 430,0 mm
t= 10.0 mm
P= 2,0 MPa
PMTA = 3,2 MPa
PSV=3,2 MPa
PTH= 4,16 MPa
Pex= 17,5 MPa.
REFERÊNCIAS BIBLIOGRÁFICAS
ASME - American Society of Mechanical Engineers, Boiler and Pressure Vessel Code, Section II Part D. New York, 2010.
BEER, F.P ; JOHNSTON, E.R; Jr; Resistência dos Materiais, 3 Edição, MAKRON Books, São Paulo.2008.
GERDAU, Catálogo de produtos Gerdau edição 2003, acessado em 13.02.2025.
GERE, James M. – Mecânica dos Materiais. Tradução: Luiz Fernado C.Paiva; revisão técnica Marco L Bittencourt – Pioneira Thomson Learning. 2003.
GROEHS, Ademar Gilberto. Resistência dos Materiais e Vasos de Pressão. São Leopoldo.2 ª Ed. RS: Editora Unisinos, 2006.
HIBBELER, R. C. Resistência dos Materiais, 7ª ed. São Paulo, Pearson, 2010.
MOTT, Robert L, UNTENER, Joseph Applied Strength of Materials, SI Units Version 6th Edition, Boca Raton: Taylor & Francis, CRC press, 2018.
NR-13 Caldeira, Vasos de Pressão e Tubulação disponível em http://trabalho.gov.br acessado em 22.11.2017.
PORTARIA MTP no.1846 de 01.07.2022 aprova a nova redacao da NR-13
TELLES, Pedro C. da Silva. Vasos de Pressão. 2ª ed. Livros Técnicos e Científicos, 1996.
TELLES, Pedro C. da Silva. Tubulações Industriais, Cálculo. 9ª ed. Livros Técnicos e Científicos 1999.